Trực tâm của tam giác là gì? Định nghĩa và tính chất chi tiết

Tam giác là một hình học cơ bản và thú vị trong toán học, và một trong các đặc điểm quan trọng của tam giác là trực tâm. Vậy, Trực Tâm Của Tam Giác Là Gì và có những tính chất nào đặc sắc? Hãy cùng tìm hiểu chi tiết về khái niệm này.

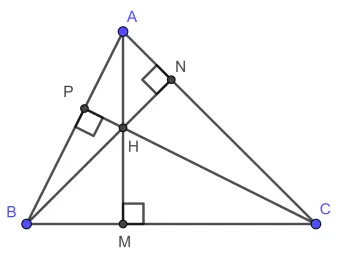
Trực tâm, được định nghĩa là giao điểm của ba đường cao trong một tam giác. Đường cao là đường thẳng đi từ một đỉnh của tam giác và vuông góc với cạnh đối diện.

Trực tâm và đường cao của tam giác

Định nghĩa Trực tâm

Trong một tam giác ABC, ba đường cao là AM, BN và CP. Giao điểm của chúng, H, được gọi là trực tâm của tam giác ABC. Vị trí của trực tâm phụ thuộc vào loại tam giác:

• Trong tam giác nhọn, trực tâm nằm bên trong tam giác.
• Trong tam giác tù, trực tâm nằm bên ngoài tam giác.
• Trong tam giác vuông, trực tâm chính là đỉnh góc vuông của tam giác.

Tính chất của Trực tâm

Trực tâm của một tam giác có nhiều tính chất đáng chú ý, đặc biệt trong tam giác đều, trực tâm, trọng tâm, tâm đường tròn nội tiếp và tâm đường tròn ngoại tiếp trùng nhau. Ngoài ra, trực tâm còn có một số ứng dụng quan trọng trong hình học và giải tích toán học.

Ví dụ Minh Họa

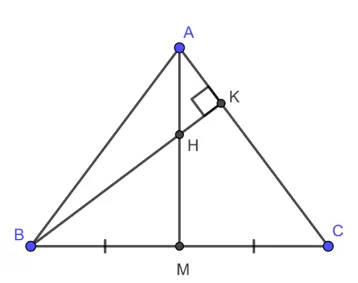
Cho tam giác ABC cân tại A, với đường trung tuyến AM và đường cao BK. Gọi H là giao điểm của AM và BK. Chứng minh rằng CH vuông góc với AB.

Ví dụ minh họa về trực tâm

Hướng dẫn:

Vì tam giác ABC cân tại A nên đường trung tuyến AM cũng là đường cao của tam giác ABC. Điều này có nghĩa rằng H là trực tâm của tam giác và từ đó suy ra CH là đường cao của tam giác, dẫn đến CH vuông góc với AB.

Để đạt được hiểu biết sâu hơn về các khái niệm liên quan, bạn có thể khám phá thêm các bài viết về định nghĩa và tính chất của tam giác.

Tài liệu Tham Khảo và Liên Kết Nội Bộ

Để hiểu sâu hơn về các khía cạnh khác của toán học và hình học, bạn có thể tham khảo các tài liệu sau qua các liên kết nội bộ của hongngu1.edu.vn:

• Expense là gì
• 5 diop là bao nhiêu độ

Hy vọng bài viết đã giúp bạn hiểu rõ hơn về trực tâm của tam giác và những ứng dụng quan trọng của nó trong học tập. Trực tâm không chỉ đơn giản là một điểm hình học, mà còn mở ra cánh cửa đến những kiến thức thú vị và phức tạp hơn trong toán học.