R trong toán học là gì? Khám phá số thực và ứng dụng của nó

Trong chương trình toán học phổ thông, khái niệm số thực R được xem là nền tảng quan trọng để giải quyết nhiều vấn đề phức tạp trong toán học. Từ các bài toán cơ bản đến những ứng dụng phức tạp, số thực luôn là một phần không thể thiếu. Hãy cùng khám phá chi tiết về số thực R và những ứng dụng của nó trong toán học.

Số thực R là gì? Định nghĩa cơ bản và ý nghĩa

Số thực, kí hiệu là R, là tập hợp bao gồm cả số hữu tỉ và số vô tỉ. Tất cả các số mà chúng ta đã học, bao gồm tập hợp số tự nhiên (N = {0, 1, 2,…}), tập số nguyên (Z = {…-3, -2, -1, 0, 1, 2,…}) và cả các số vô tỉ, đều là thành phần của số thực. Một cách tổng quát:

Tập hợp số tự nhiên, ký hiệu N: {0, 1, 2, 3, …}
Tập hợp số nguyên, ký hiệu Z: {…, -3, -2, -1, 0, 1, 2, …}
Tập hợp số hữu tỉ, ký hiệu Q: {a/b; a, b ∈ Z, b ≠ 0}
Tập hợp số vô tỉ, ký hiệu I: Số thập phân không tuần hoàn

Tập hợp các số thực R là sự kết hợp giữa các tập hợp này: R = Q ∪ I. Như vậy, mọi con số chúng ta biết đều có thể được tìm thấy trong tập hợp số thực R.

Biểu diễn tập hợp số thực

Những tính chất nổi bật của tập hợp số thực R

Số thực có nhiều tính chất quan trọng, giúp giải quyết các phép tính và bài toán phức tạp:

Mỗi số thực có thể là số âm hoặc số dương, trừ trường hợp là số 0.
Tổng và tích của hai số thực không âm luôn là không âm.
Số thực là một tập hợp vô hạn, không đếm được tất cả các số.
Số thực giúp biểu diễn các phép đo đại lượng liên tục và có thể biểu thị dưới dạng số thập phân.

Ngoài ra, các số thực cũng được sử dụng rộng rãi trong các phép toán như cộng, trừ, nhân và chia (trừ chia cho 0), và có thể sắp xếp tuyến tính trên trục số.

Thuộc tính và ứng dụng của số thực trong toán học

Một số thuộc tính của tập hợp số thực bao gồm:

Phép cộng và phép nhân của số thực đúng đắn dưới định nghĩa số mũ và căn số.
Trong một tập hợp số thực không rỗng với cận trên, cận trên chính chắc chắn là một số thực nhỏ nhất.

Thuộc tính của số thực

Bài tập minh họa về số thực

Ví dụ 1: Điền vào dấu (∈, ∉, ⊂) thích hợp vào chỗ trống

Đáp án:

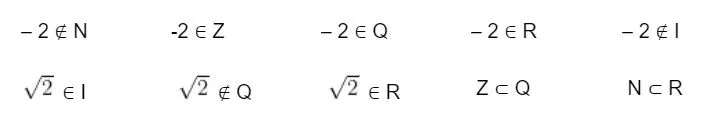Câu hỏi ví dụ về số thực

Ví dụ 2: Sắp xếp các số thực sau theo thứ tự tăng dần:

0,466; 7/15; 0,4636363…; 0,463736; 0,4656365…

Đáp án: 0,463736 < 0,4636363… < 7/15 < 0,4656365… < 0,466

Ví dụ 3: Tìm các tập hợp sau:

a) Q ∩ I ;

b) R ∩ I.

Đáp án:

a) Q ∩ I = Ø ;

b) R ∩ I = I

Ví dụ 4: Tìm x, biết 3,2.x + (-1,2).x +2,7 = -4,9

Giải:

[3,2 + (-1,2)].x + 2,7 = -4,9

2.x + 2,7 = – 4,9

2.x = – 4,9 – 2,7

2.x = – 7,6

x = -7,6 : 2

x = -3,8

Tập hợp số cần ghi nhớ trong toán học

Tập hợp số tự nhiên (N)

Các số tự nhiên bao gồm: 0, 1, 2, 3, 4, 5, …

Tập hợp số nguyên (Z)

Số nguyên bao gồm các số: …, -3, -2, -1, 0, 1, 2, 3, …

Tập hợp số hữu tỉ (Q)

Tập hợp số hữu tỉ bao gồm tất cả các số có dạng a/b với a, b là số nguyên, b ≠ 0.

Tập hợp số thực (R)

Số thực gồm cả số hữu tỉ và số vô tỉ. Một số vô tỉ biểu diễn bởi số thập phân vô hạn không tuần hoàn.

Bạn có thể tìm hiểu thêm về khái niệm số thực qua bài viết Hướng dẫn cách vẽ tranh an toàn giao thông. Với kiến thức từ bài viết này, hy vọng bạn sẽ tự tin hơn khi được hỏi “R Trong Toán Học Là Gì?”. Hãy tiếp tục khám phá thế giới toán học và ứng dụng thực tiễn của nó!