Mod là gì trong Toán học? Ứng dụng và Bài tập

Bạn đang tìm hiểu về khái niệm “mod” trong toán học? Bài viết này từ THPT Hồng Ngự 1 sẽ giải đáp chi tiết Mod Là Gì Trong Toán Học, cùng với các ứng dụng thực tế và các dạng bài tập thường gặp.

Mod là gì trong Toán học?

Trong toán học, “mod” (viết tắt của “modulo”) là một phép toán tìm phần dư của một phép chia. Khi chia một số nguyên a cho một số nguyên b, phần dư là số còn lại sau khi thực hiện phép chia. Phép toán này được ký hiệu là a mod b, và kết quả được tính bằng công thức: a mod b = a - (b * q), trong đó q là thương nguyên của phép chia a cho b (phần nguyên của a/b).

Ví dụ: 10 mod 3 = 1 (vì 10 chia 3 được 3 dư 1).

Phép toán Modulo giúp xác định phần dư của phép chia

Phép toán modulo có nhiều ứng dụng quan trọng trong các lĩnh vực khác nhau:

• Toán học thuần túy: Sử dụng trong lý thuyết số, đặc biệt trong việc xác định tính chia hết.
• Lập trình máy tính: Xác định vị trí phần tử trong mảng, tính ngày trong tuần, tạo chu kỳ trong thuật toán.
• Mật mã học: Mã hóa và giải mã thông tin.
• Tính toán hợp đồng thông minh: Quản lý thời gian và giao dịch trên blockchain.
• Khoa học máy tính: Thuật toán hashing, kiểm tra bảo mật.

Vậy, bạn đã hiểu rõ mod là gì trong toán học rồi chứ? Tiếp theo, chúng ta sẽ cùng tìm hiểu về các tính chất quan trọng của phép toán này. Đừng quên rằng, THPT Hồng Ngự 1 luôn cập nhật những kiến thức hữu ích nhất cho bạn.

Sau khi tìm hiểu định nghĩa, để hiểu rõ hơn, bạn có thể tham khảo thêm về Analytics là gì.

Tính chất của Mod trong Toán học

Phép toán modulo sở hữu nhiều tính chất quan trọng, giúp chúng ta sử dụng nó một cách hiệu quả trong giải toán và lập trình:

1. Tính kết hợp: Không đúng. (a mod b) mod c ≠ a mod (b * c).
2. Tính chia nhỏ: Nếu a ≡ b (mod c) và x ≡ y (mod c), thì (a + x) ≡ (b + y) (mod c) và (a * x) ≡ (b * y) (mod c).
3. Tính đối xứng: a ≡ b (mod m) nếu và chỉ nếu b ≡ a (mod m).
4. Tính phân phối: (a + b) mod c = [(a mod c) + (b mod c)] mod c và (a * b) mod c = [(a mod c) * (b mod c)] mod c.
5. Phép mũ: a^x ≡ (a mod m)^x (mod m).
6. Tính chia hết: a chia hết cho m khi và chỉ khi a ≡ 0 (mod m).

Các tính chất này giúp ta hiểu rõ hơn về cách hoạt động của phép toán modulo và cách áp dụng nó trong các bài toán. Đồng thời, chúng cũng hữu ích trong việc chứng minh và giải quyết các bài toán liên quan đến phép toán modulo. Ví dụ, tính chất chia nhỏ rất hữu ích khi bạn muốn tính Pascal là gì trong các bài toán tổ hợp.

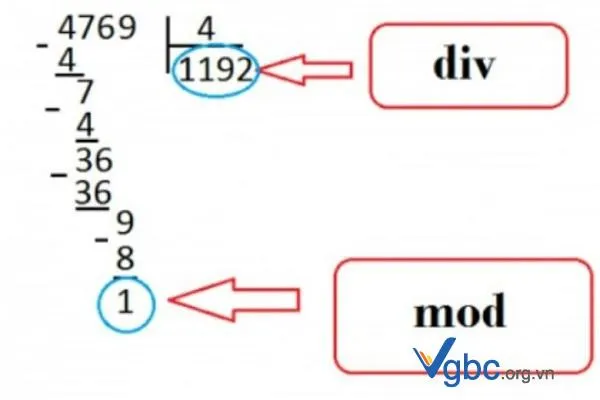Các dạng bài toán thường gặp về Mod trong Toán học

Các Dạng Bài Tập Thường Gặp về Mod

Có rất nhiều dạng bài tập khác nhau liên quan đến phép toán mod. Dưới đây là một số dạng bài phổ biến:

1. Tính phần dư: Tính a mod b với a và b cho trước. Ví dụ: 25 mod 7 = 4.
2. Kiểm tra tính chia hết: Xác định xem a có chia hết cho b hay không bằng cách kiểm tra xem a mod b có bằng 0 hay không.
3. Tìm chu kỳ của dãy số: Tìm chu kỳ của một dãy số sau khi thực hiện phép toán modulo. Ví dụ: Dãy Fibonacci mod 5.
4. Giải mã: Giải mã thông điệp đã được mã hóa bằng cách sử dụng phép toán mod và một khóa cho trước.
5. Ứng dụng trong lịch: Xác định ngày trong tuần dựa trên một ngày cho trước.
6. Tính toán nhị phân: Sử dụng phép toán mod để thực hiện các phép tính trong hệ nhị phân.

Để hiểu rõ hơn về ứng dụng của các mô hình mạng, bạn có thể tìm hiểu thêm về mô hình mạng phổ biến hiện nay là gì. Bên cạnh đó, trong vật lý, động phản quang học là gì cũng là một kiến thức thú vị liên quan đến tính chất tuần hoàn, có thể liên hệ với chu kỳ trong phép mod.

Kết luận

Hy vọng bài viết này đã giúp bạn hiểu rõ mod là gì trong toán học, các tính chất quan trọng và các ứng dụng thực tế của nó. Phép toán modulo là một công cụ mạnh mẽ, được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau. Hãy luyện tập giải các bài tập để nắm vững kiến thức này và áp dụng nó một cách hiệu quả. Chúc bạn học tốt!