Arctan là gì? Định nghĩa và Công thức Đạo hàm Arctan trong Toán Học

Arctan Là Gì? Đây là câu hỏi thường gặp của học sinh khi bắt đầu tìm hiểu về lượng giác và đạo hàm. Bài viết này của THPT Hồng Ngự 1 sẽ giải đáp chi tiết về Arctan, cùng với các công thức đạo hàm Arctan thường gặp trong chương trình giáo dục phổ thông.

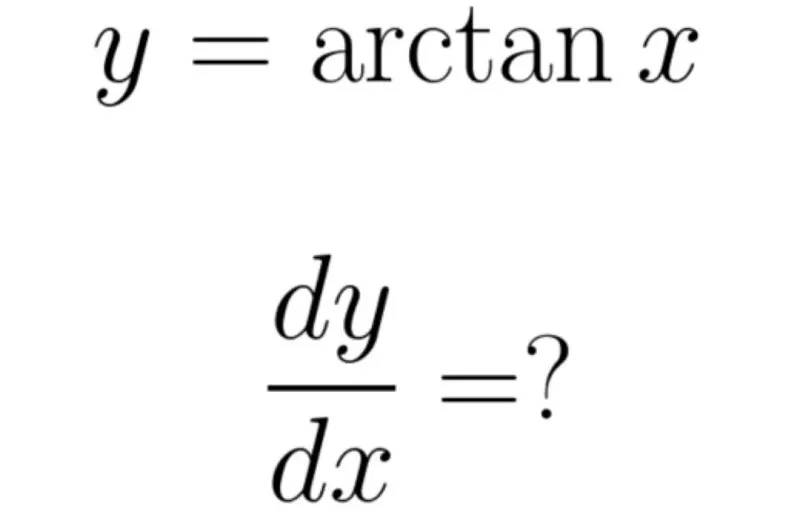Công thức tính đạo hàm arctan x thường gặp nhất hiện nay. (Ảnh: Sưu tầm Internet)

Arctan là gì? Khái niệm Hàm Arctan

Arctan, viết tắt của “arctangent”, là hàm số ngược của hàm tangent (tan). Nói cách khác, nếu tan(y) = x, thì arctan(x) = y. Để tồn tại hàm số ngược, hàm số gốc phải thỏa mãn một trong hai điều kiện: là ánh xạ 1-1 hoặc đơn điệu tăng/giảm chặt trên một khoảng xác định.

Các Công thức Tính Đạo hàm Arctan Thường Gặp

Dưới đây là một số công thức đạo hàm Arctan thường gặp trong chương trình học phổ thông:

1. Đạo hàm của hàm số y = arctan x

Hàm số y = arctan x được định nghĩa trên tập số thực. Khi tan(y) = x, thì arctan(x) là hàm ngược của tan(x).

Công thức:

Nếu y = arctan x thì:

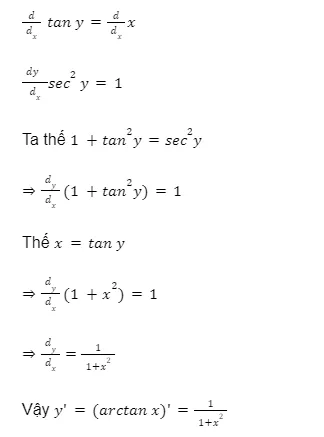
Ví dụ:

Tính đạo hàm của y = arctan x.

Lời giải:

Vì y = arctan x nên tan y = x. Lấy đạo hàm hai vế theo biến x, ta được:

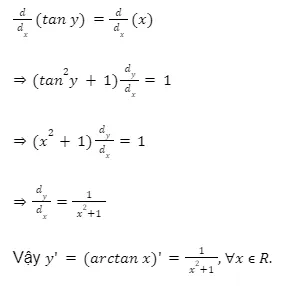
2. Đạo hàm của hàm số y = arctan(u) – Hàm Hợp của Arctan

Đây là hàm hợp của hàm Arctan với một hàm số khác u(x).

Công thức:

Nếu y = arctan(u) với u là một hàm của x thì:
(y’) = (u’)/(1+u^2)

Ví dụ:

Tính đạo hàm của y = x^2.arcsin(x).

Lời giải:

Áp dụng công thức đạo hàm của hàm hợp và đạo hàm của arcsin(x), ta có:

3. Đạo hàm của hàm số arctan(x/y)

Công thức:

Công thức đạo hàm này phức tạp hơn và ít gặp trong chương trình phổ thông.

Ví dụ:

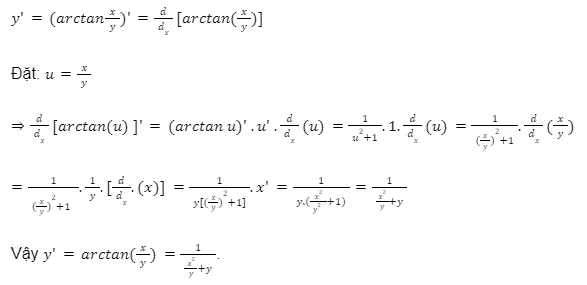
Bài Tập Tự Luyện về Đạo Hàm Arctan

Dưới đây là một số bài tập tự luyện để củng cố kiến thức về đạo hàm Arctan:

Bài tập 1, 2, 3, 4, 5, 6: (Chèn hình ảnh lời giải của từng bài tập tương ứng từ bài gốc)

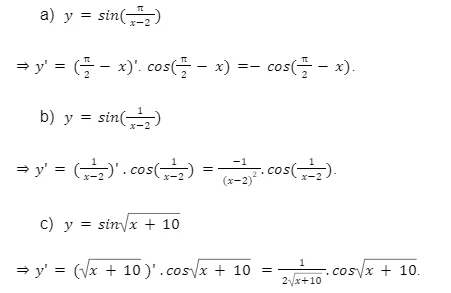
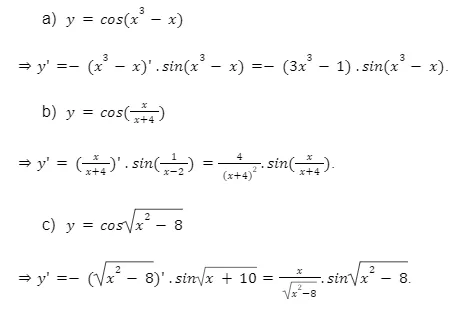
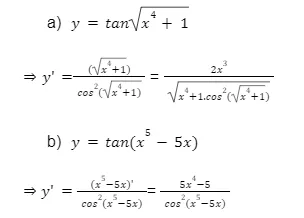
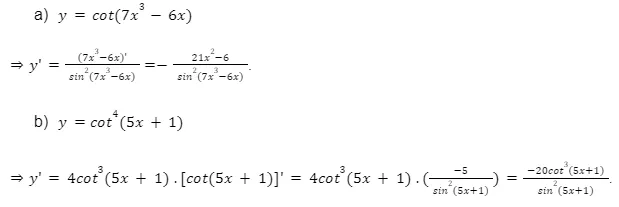
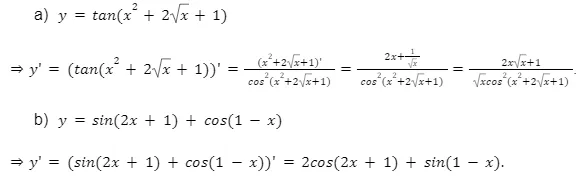
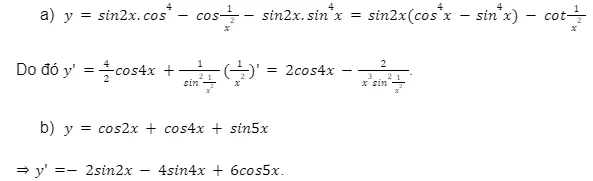
Kết luận

Hiểu rõ khái niệm Arctan và các công thức đạo hàm liên quan là nền tảng quan trọng để giải quyết các bài toán trong lượng giác và giải tích. Hy vọng bài viết của THPT Hồng Ngự 1 đã giúp bạn hiểu rõ hơn về “Arctan là gì” và cách tính đạo hàm của nó.