Tứ Giác Là Gì? Tổng Quan Kiến Thức Về Tứ Giác Dành Cho Học Sinh

Hình tứ giác là một khái niệm quen thuộc trong hình học phẳng, xuất hiện rất nhiều trong chương trình học phổ thông và các ứng dụng thực tế. Vậy Tứ Giác Là Gì? Bài viết này của THPT Hồng Ngự 1 sẽ cung cấp một cái nhìn tổng quan và chi tiết nhất về tứ giác, từ định nghĩa, phân loại, tính chất đến các dạng đặc biệt và công thức tính toán liên quan.

Định Nghĩa Hình Tứ Giác

Hình tứ giác là một đa giác có bốn đỉnh và bốn cạnh, trong đó không có bất kỳ hai cạnh nào cùng nằm trên một đường thẳng.

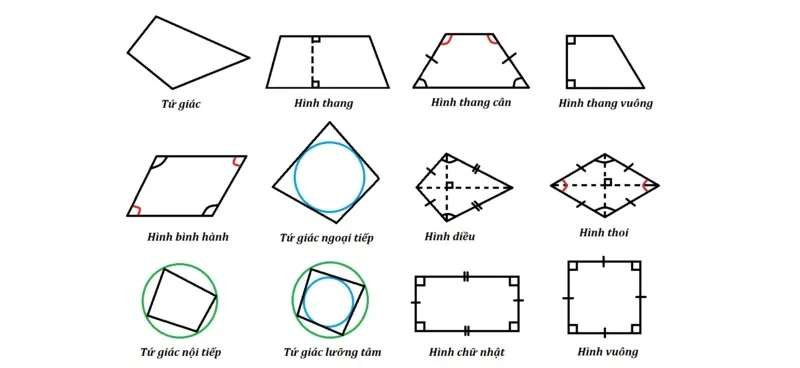Hình ảnh minh họa các dạng tứ giác khác nhau

Tứ giác là một hình học phổ biến, được ứng dụng rộng rãi trong nhiều lĩnh vực.

Phân loại: Tứ giác có thể là tứ giác lồi (convex quadrilateral) hoặc tứ giác lõm (concave quadrilateral), tùy thuộc vào vị trí tương đối của các đỉnh và cạnh.

Ký hiệu: Hình tứ giác thường được ký hiệu bằng bốn chữ cái in hoa, ví dụ như ABCD, tương ứng với tên của bốn đỉnh của nó.

Tổng số đo các góc trong của một hình tứ giác luôn bằng 360 độ: ∠A + ∠B + ∠C + ∠D = 360°. Hiểu rõ điều này sẽ giúp ích rất nhiều trong giải toán. Bạn có thể tham khảo thêm về cách làm bình đắp đá tự chế để hiểu thêm về các ứng dụng hình học trong đời sống.

Tính Chất Quan Trọng Của Tứ Giác

Khi tìm hiểu tứ giác là gì, cần nắm vững hai tính chất cơ bản sau:

Tính chất 1 (Đường chéo):

Trong một tứ giác lồi, hai đường chéo cắt nhau tại một điểm nằm bên trong tứ giác.
Ngược lại, nếu hai đường chéo của một tứ giác cắt nhau tại một điểm nằm bên trong tứ giác đó, thì tứ giác đó là tứ giác lồi.

Tính chất 2 (Góc): Tổng số đo của bốn góc trong một hình tứ giác luôn bằng 360°. Đây là một tính chất quan trọng giúp giải nhiều bài toán liên quan đến tứ giác.

Phân Loại Các Dạng Tứ Giác Thường Gặp

Tứ giác có thể được phân loại thành nhiều dạng khác nhau, mỗi dạng có những đặc điểm và tính chất riêng biệt:

Tứ giác đơn: Là tứ giác mà các cạnh không cắt nhau tại bất kỳ điểm nào khác ngoài các đỉnh.
Tứ giác lõm: Là tứ giác có ít nhất một góc lớn hơn 180°. Một trong hai đường chéo của tứ giác lõm nằm bên ngoài hình.
Tứ giác lồi: Là tứ giác mà tất cả các góc đều nhỏ hơn 180°. Cả hai đường chéo đều nằm hoàn toàn bên trong hình.

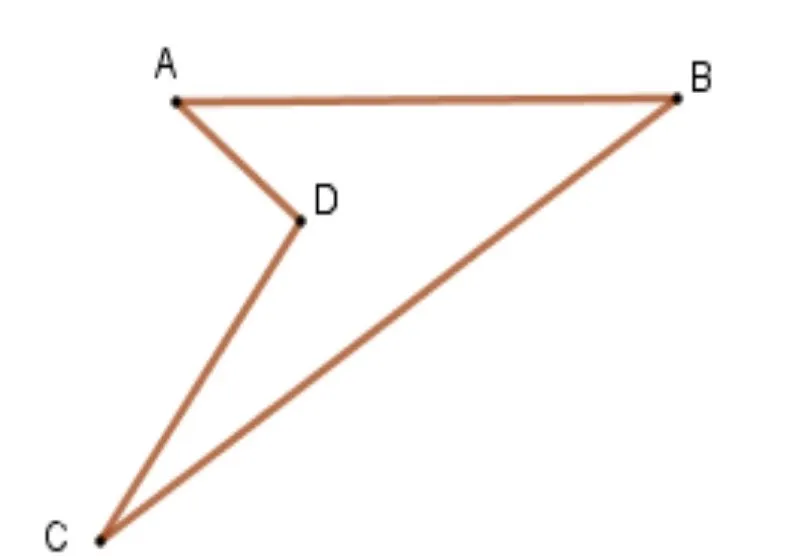Hình ảnh minh họa tứ giác lồi
Tứ giác không đều: Là tứ giác không có cặp cạnh nào song song với nhau và không có tính đối xứng đặc biệt.

Ngoài ra, còn có các dạng tứ giác đặc biệt:

Các Dạng Tứ Giác Đặc Biệt

Hình thang: Là tứ giác có ít nhất một cặp cạnh đối song song.
Hình thang cân: Là hình thang có hai góc kề một đáy bằng nhau. Hình thang cân cũng có hai đường chéo bằng nhau.
Hình bình hành: Là tứ giác có các cặp cạnh đối song song và bằng nhau. Hình bình hành có các góc đối bằng nhau và hai đường chéo cắt nhau tại trung điểm của mỗi đường. Tham khảo thêm về lịch sử để biết thêm thông tin thú vị về các khái niệm toán học như năm 1922 là năm con gì.

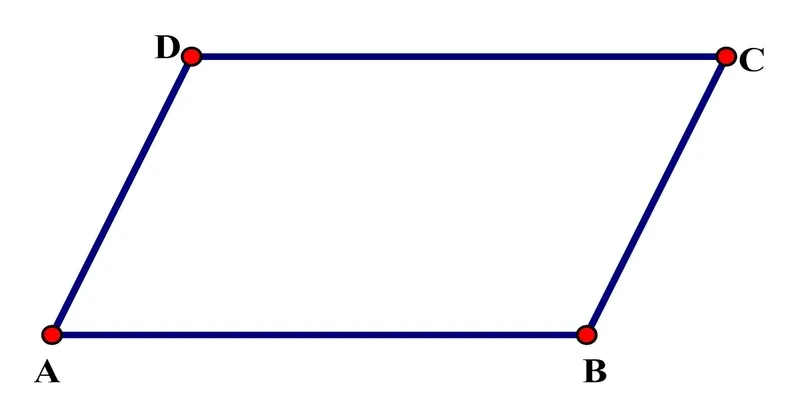Hình ảnh minh họa hình bình hành
Hình thoi: Là tứ giác có bốn cạnh bằng nhau. Hình thoi có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
Hình chữ nhật: Là tứ giác có bốn góc vuông. Hình chữ nhật có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Hình vuông: Là tứ giác có bốn góc vuông và bốn cạnh bằng nhau. Hình vuông là trường hợp đặc biệt của cả hình chữ nhật và hình thoi.
Tứ giác nội tiếp: Là tứ giác có bốn đỉnh nằm trên cùng một đường tròn. Tổng hai góc đối của tứ giác nội tiếp bằng 180°. Đôi khi, học tập cũng cần chút thư giãn, bạn có thể tìm hiểu thêm về Nhạc sống Delta là gì để giải tỏa căng thẳng.

Công Thức Tính Chu Vi Và Diện Tích Tứ Giác

Khi đã hiểu rõ tứ giác là gì, việc nắm vững các công thức tính chu vi và diện tích là vô cùng quan trọng.

Công thức tính chu vi

Chu vi của tứ giác là tổng độ dài của bốn cạnh:

P = a + b + c + d

Trong đó:

P: Chu vi tứ giác
a, b, c, d: Độ dài các cạnh của tứ giác

Công thức tính diện tích

Diện tích của tứ giác phụ thuộc vào từng dạng hình cụ thể:

Hình vuông: S = a x a (a là độ dài cạnh)
Hình chữ nhật: S = a x b (a là chiều dài, b là chiều rộng)
Hình bình hành: S = a x h (a là độ dài cạnh đáy, h là chiều cao)

Để hiểu rõ hơn, bạn có thể tham khảo thêm về la hán đẩy xe bò là gì để liên hệ với các bài toán thực tế.

Mẹo Ghi Nhớ Kiến Thức Về Tứ Giác Hiệu Quả

Nắm vững định nghĩa và phân loại: Hiểu rõ tứ giác là gì và các dạng của nó là nền tảng để giải quyết các bài toán.
Học thông qua hình ảnh và ví dụ thực tế: Sử dụng hình ảnh minh họa và liên hệ với các vật thể quen thuộc trong cuộc sống để ghi nhớ các dạng tứ giác và tính chất của chúng.

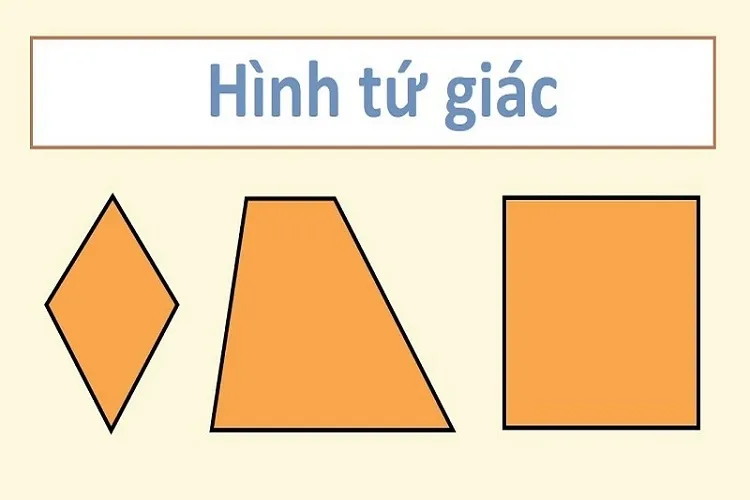Hình ảnh minh họa các dạng tứ giác thường gặp trong thực tế
Luyện tập thường xuyên: Giải nhiều bài tập từ cơ bản đến nâng cao để làm quen với các dạng toán và rèn luyện kỹ năng giải quyết vấn đề.
Sử dụng phần mềm và ứng dụng học tập: Các ứng dụng học toán có thể giúp việc học trở nên thú vị và hiệu quả hơn.
Học nhóm và trao đổi kiến thức với bạn bè: Trao đổi kiến thức với bạn bè giúp bạn hiểu sâu hơn và phát hiện ra những lỗ hổng trong kiến thức của mình. Đôi khi, những điều tưởng chừng đơn giản lại có ý nghĩa lớn, giống như việc tìm hiểu honey là gì trong một bài học ngôn ngữ.

Kết Luận

Hiểu rõ tứ giác là gì, các tính chất và phân loại của chúng là rất quan trọng trong học tập và ứng dụng thực tế. Hy vọng bài viết này của THPT Hồng Ngự 1 đã cung cấp cho bạn một cái nhìn tổng quan và chi tiết nhất về tứ giác. Hãy tiếp tục học tập và khám phá thêm nhiều kiến thức thú vị khác về hình học nhé!