Góc Đồng Vị Là Gì? Khám Phá Khái Niệm và Cách Xác Định

Góc đồng vị là khái niệm quan trọng trong toán học, thường xuất hiện trong các bài học về góc và đường thẳng song song. Để nắm vững khái niệm này, hãy cùng tìm hiểu cách xác định các cặp góc đồng vị thông qua bài viết dưới đây.

Trong hình học, khi một đường thẳng cắt hai đường thẳng khác, các góc được tạo ra có thể được sắp xếp thành các cặp đặc biệt. Dưới đây chúng ta sẽ khám phá các cặp góc so le trong, góc đồng vị và góc trong cùng phía.

Cách Xác Định Các Cặp Góc

1. Cặp Góc So Le Trong

Để xác định cặp góc so le trong, chúng ta dựa vào hai đường thẳng bị cắt bởi một đường thẳng thứ ba. Hai góc ở vị trí so le và nằm trong khu vực giữa hai đường thẳng song song này được gọi là góc so le trong.

2. Cặp Góc Đồng Vị

Cặp góc đồng vị là khi hai góc nằm cùng một phía của đường cắt và có vị trí tương ứng ở mỗi đường thẳng mà đường cắt này giao nhau. Dưới đây là ví dụ minh họa:

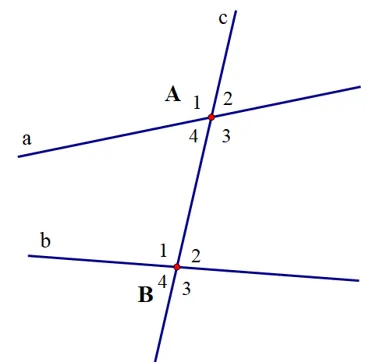Ví dụ góc đồng vị

Trong hình trên, các cặp góc đồng vị bao gồm: góc ( A_1 ) và ( B_1 ), góc ( A_2 ) và ( B_2 ), góc ( A_3 ) và ( B_3 ), cũng như góc ( A_4 ) và ( B_4 ).

3. Cặp Góc Trong Cùng Phía

Góc trong cùng phía là hai góc nằm ở bên trong của hai đường thẳng và cùng phía của đường cắt. Ví dụ, góc ( A_4 ) và góc ( B_1 ) là một cặp góc trong cùng phía trong hình trên.

Để tìm hiểu thêm về các khái niệm tương tự hoặc gặp khó khăn trong học tập, bạn có thể xem thêm thông tin về các ngày đặc biệt như Ngày 26/3 là ngày gì để thư giãn đầu óc và tái tạo năng lượng học tập.

Ví Dụ Minh Họa

Ví Dụ 1

Cho đường thẳng ( xy ) cắt hai đường thẳng ( ab ) và ( cd ) tại hai điểm ( M ) và ( N ). Xác định:

• Hai cặp góc so le trong: ( aMN^ ) và ( MNd^ ); ( bMN^ ) và ( MNc^ ).
• Bốn cặp góc đồng vị: ( xMa^ ) và ( MNc^ ); ( xMb^ ) và ( MNd^ ); ( aMN^ ) và ( cNy^ ); ( bMN^ ) và ( dNy^ ).
• Hai cặp góc trong cùng phía: ( aMN^ ) và ( MNc^ ); ( bMN^ ) và ( MNd^ ).

Ví dụ minh họa

Ví Dụ 2

Điền vào chỗ trống trong các câu sau:

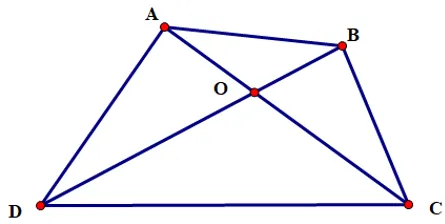
• ( BAC^ ) và ( ACD^ ) là một cặp góc so le trong.
• ( BAO^ ) và ( BOC^ ) là một cặp góc đồng vị.
• ( DAC^ ) và ( ACB^ ) là một cặp góc so le trong.
• ( AOD^ ) và ( OCD^ ) là một cặp góc đồng vị.

Lời Kết

Hiểu được cách xác định các loại góc như góc đồng vị, góc so le trong và góc trong cùng phía sẽ giúp bạn nắm vững hơn kiến thức hình học cơ bản. Điều này không chỉ hữu ích trong học tập mà còn trong việc giải quyết các vấn đề thực tế. Nếu cần thêm tài liệu học tập, đừng quên truy cập THPT Hồng Ngự 1 để tìm kiếm thông tin hữu ích nhất.