Bạn đã bao giờ tự hỏi “3 đường Thẳng đồng Quy Là Gì?” trong hình học? Đây là một khái niệm cơ bản nhưng quan trọng, xuất hiện thường xuyên trong các bài toán hình học phẳng. Bài viết này của THPT Hồng Ngự 1 sẽ giúp bạn hiểu rõ về định nghĩa, các trường hợp thường gặp, phương pháp chứng minh và bài tập thực tế liên quan đến tính đồng quy. Cùng khám phá nhé!
Định nghĩa đồng quy
Trong hình học, đồng quy dùng để chỉ tình trạng ba hoặc nhiều đường thẳng cùng giao nhau tại một điểm duy nhất. Điểm giao nhau này được gọi là điểm đồng quy. Tính chất đồng quy là một kiến thức nền tảng, có vai trò quan trọng trong cả hình học phẳng và hình học không gian. Ứng dụng của nó rất đa dạng, từ việc chứng minh các định lý đến giải quyết các bài toán liên quan đến đường thẳng, tam giác, và nhiều hình học khác.
 Đồng quy là việc ba hoặc nhiều đường thẳng giao nhau tại một điểm
Đồng quy là việc ba hoặc nhiều đường thẳng giao nhau tại một điểm
Ngoài ra, tính chất đồng quy còn được ứng dụng trong các lĩnh vực thực tế như kiến trúc, thiết kế cầu đường và nhiều ngành kỹ thuật khác. Nếu bạn đang tìm kiếm sách luyện viết chữ đẹp cho người lớn, hãy ghé thăm website của chúng tôi để khám phá những tài liệu hữu ích.
Các trường hợp đồng quy thường gặp
Tính chất đồng quy không chỉ giới hạn trong tam giác mà còn xuất hiện ở nhiều dạng hình khác nhau, bao gồm đường tròn, tứ giác, và thậm chí cả trong không gian ba chiều. Dưới đây là một số trường hợp đồng quy thường gặp:
 Một số trường hợp đồng quy thường gặp
Một số trường hợp đồng quy thường gặp
- Đường đồng quy trong tam giác: Các đường trung tuyến, đường phân giác, đường trung trực hoặc đường cao xuất phát từ các đỉnh của tam giác đều có thể đồng quy.
- Đường đồng quy trong hình tròn: Tất cả các đường kính của một đường tròn đều đồng quy tại tâm của đường tròn. Tương tự, tất cả các tiếp tuyến tại một điểm trên đường tròn cũng đồng quy tại điểm đó.
Hiểu rõ các trường hợp này sẽ giúp bạn dễ dàng nhận biết và giải quyết các bài toán liên quan đến tính đồng quy.
Các phương pháp chứng minh đồng quy
Chứng minh 3 đường thẳng đồng quy là một dạng bài tập phổ biến trong hình học. Để giải quyết dạng bài này, bạn cần nắm vững các phương pháp sau:
- Phương pháp 1: Tìm giao điểm của hai đường thẳng, sau đó chứng minh đường thẳng thứ ba đi qua giao điểm đó.
- Phương pháp 2: Chứng minh một điểm cụ thể thuộc cả ba đường thẳng cần xét.
- Phương pháp 3: Áp dụng các tính chất đồng quy đặc biệt trong tam giác, chẳng hạn như định lý Ceva hoặc định lý Menelaus.
- Phương pháp 4: Sử dụng tính chất của các đường thẳng cắt nhau, quan hệ giữa các đường song song hoặc các đoạn thẳng có tỷ lệ đặc biệt.
- Phương pháp 5: Sử dụng phương pháp phản chứng. Giả sử ba đường thẳng không đồng quy, sau đó chỉ ra mâu thuẫn với giả thiết hoặc một kết luận đã biết.
- Phương pháp 6: Dựa vào tính chất thẳng hàng của các điểm để suy ra ba đường thẳng phải cùng đi qua một điểm duy nhất.
- Phương pháp 7: Chứng minh trực tiếp rằng cả ba đường thẳng đều đi qua cùng một điểm, từ đó khẳng định tính chất đồng quy.
Nắm vững các phương pháp này giúp bạn linh hoạt hơn trong việc giải quyết các bài toán chứng minh đồng quy. Đừng quên ghé thăm THPT Hồng Ngự 1 thường xuyên để cập nhật thêm nhiều kiến thức bổ ích. Bạn có biết 20/4 là cung gì không? Hãy tìm hiểu thêm trên website của chúng tôi!
 Các phương pháp chứng minh đồng quy
Các phương pháp chứng minh đồng quy
Bài tập ví dụ về đồng quy
Để củng cố kiến thức về 3 đường thẳng đồng quy, hãy cùng xem xét một số ví dụ sau:
Dạng 1: Tìm các đường đồng quy
Cho hình vẽ sau, hãy xác định những đường thẳng đồng quy và điểm đồng quy của chúng:
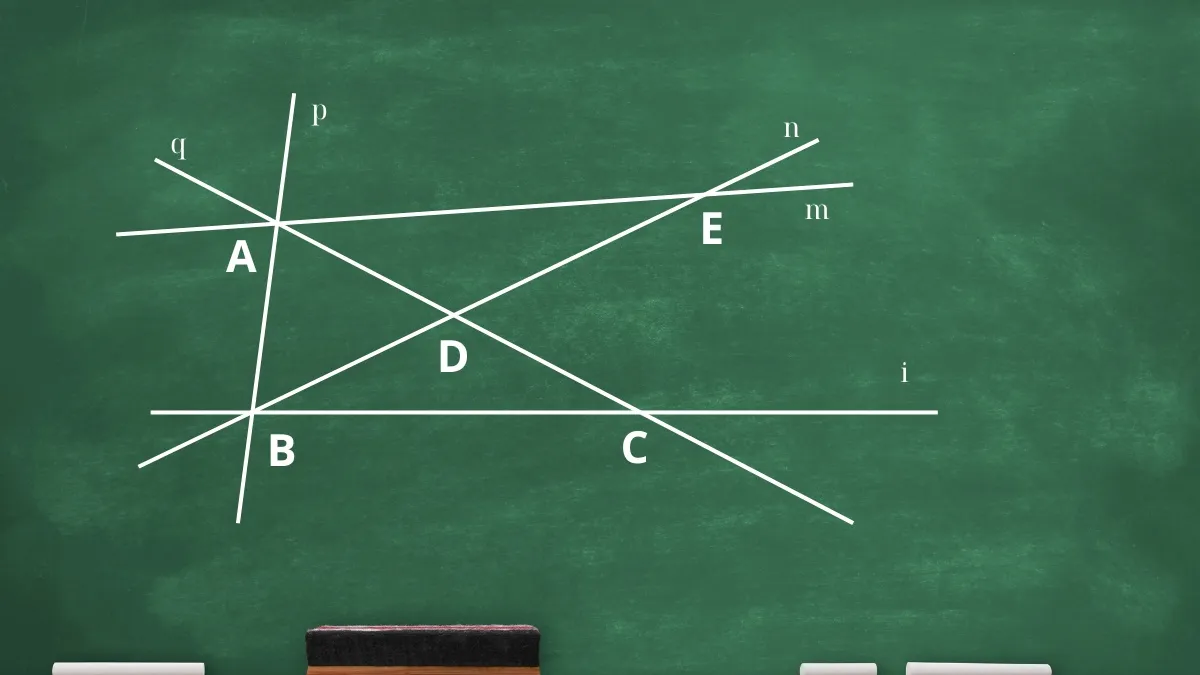 Bài tập ví dụ về dạng toán tìm các đường đồng quy
Bài tập ví dụ về dạng toán tìm các đường đồng quy
- Đường thẳng p, q và m đồng quy tại điểm A.
- Đường thẳng i, p và n đồng quy tại điểm B.
Dạng 2: Chứng minh đường thẳng đồng quy theo định thức
Cho ba phương trình đường thẳng sau:
- p: 3x – 4y – 13 = 0
- q: 8x – 11y – 33 = 0
- m: 2x – 3y – 7 = 0
Chứng minh rằng ba đường thẳng này đồng quy.
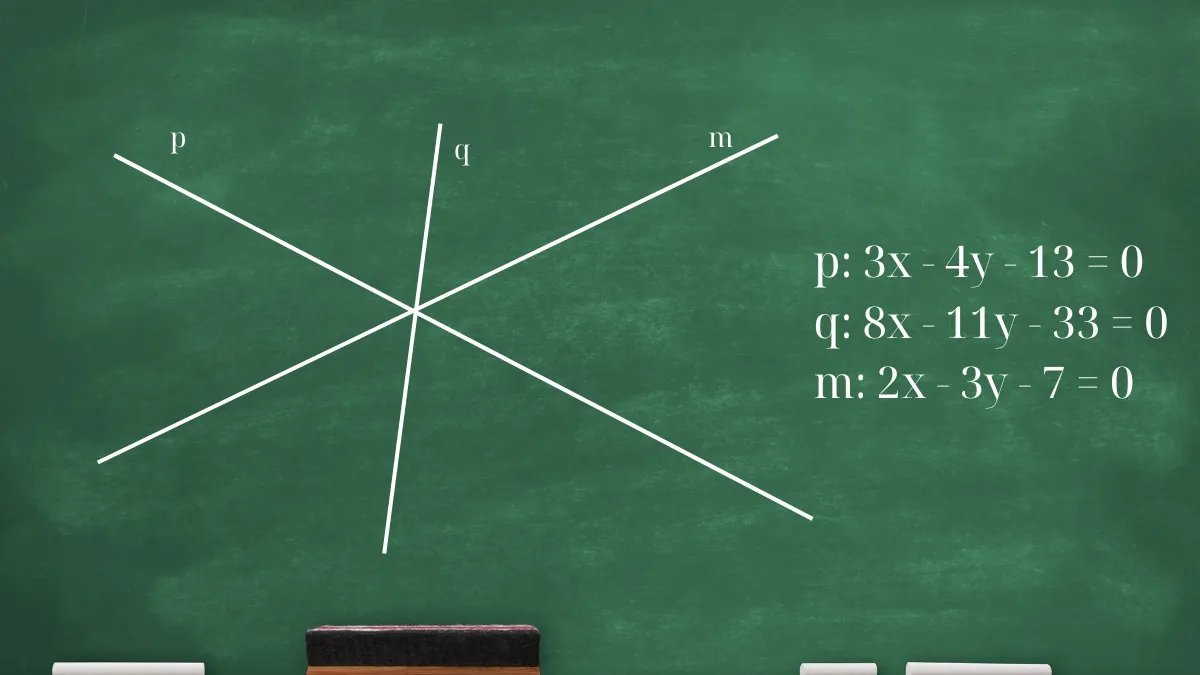 Bài tập ví dụ về dạng toán chứng minh đường thẳng đồng quy theo định thức
Bài tập ví dụ về dạng toán chứng minh đường thẳng đồng quy theo định thức
Lời giải:
Điều kiện để ba đường thẳng p, q, m đồng quy là định thức sau phải bằng 0:
D = 3*(77 – 99) – (-4)*(-56 + 6) – 13*(-24 + 22)
D = -66 + 40 + 26 = 0
Vậy, p, q, m đồng quy.
Dạng 3: Xác định đường thẳng đồng quy trong tam giác
Trong tam giác ABC, kẻ ba đường thẳng từ mỗi đỉnh, song song với cạnh đối diện. Ba đường thẳng này cắt nhau tạo thành các điểm F, D, E. Chứng minh rằng AD, BE, CF đồng quy.
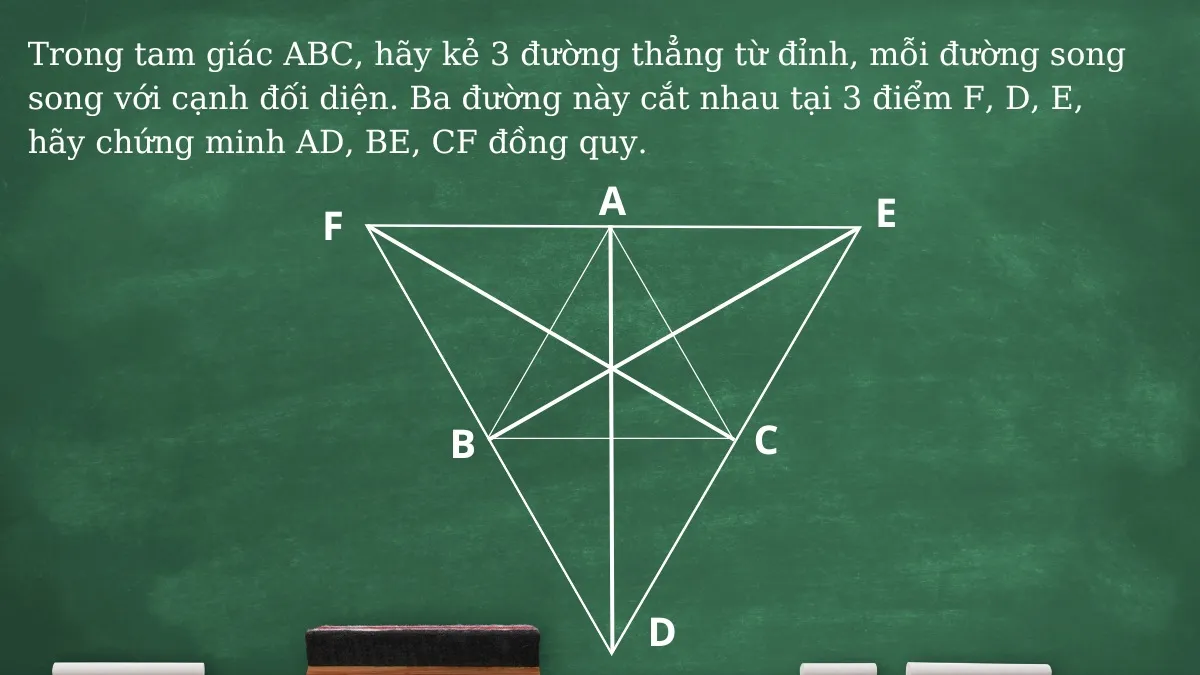 Bài tập ví dụ về dạng toán xác định đường thẳng đồng quy trong tam giác
Bài tập ví dụ về dạng toán xác định đường thẳng đồng quy trong tam giác
Lời giải:
Tứ giác ABCE có AE // BC và AB // CE, suy ra ABCE là hình bình hành. Do đó, AE = BC.
Tương tự, ACBF là hình bình hành, suy ra AF = BC. Vậy, AE = AF, tức A là trung điểm của EF.
Lý luận tương tự, DF và DE lần lượt có trung điểm là B và C.
Vậy, các cạnh của tam giác DEF có 3 trung điểm là A, B, C.
Do đó, AD, BE, CF đồng quy.
Bạn có muốn biết 23/1 là cung gì? Hãy truy cập website THPT Hồng Ngự 1 để tìm hiểu thêm những điều thú vị.
Ứng dụng thực tế của đồng quy
Tính chất đồng quy không chỉ là một khái niệm trừu tượng trong hình học mà còn có nhiều ứng dụng trong thực tế, bao gồm:
 Ứng dụng của đồng quy trong thực tế
Ứng dụng của đồng quy trong thực tế
- Kiến trúc & xây dựng: Ứng dụng trong thiết kế nhà cửa, cầu, mái vòm, hệ thống giàn giáo để phân bổ lực cân bằng và đảm bảo tính ổn định của công trình.
- Cơ học: Tính toán cân bằng lực trong máy móc, cần cẩu, giúp đảm bảo hoạt động an toàn và hiệu quả.
- Quang học: Ứng dụng trong quy tắc phối cảnh trong nhiếp ảnh, thiết kế ống kính, tạo ra những hình ảnh chân thực và sống động.
- Vận tải: Quy hoạch vòng xuyến, điểm nút giao thông, giúp tối ưu hóa luồng giao thông và giảm thiểu ùn tắc.
- Hội họa & điêu khắc: Tạo bố cục và sáng tạo các tác phẩm có chiều sâu, mang đến những trải nghiệm nghệ thuật độc đáo.
Bạn có tin vào điềm báo từ giấc mơ? Tìm hiểu ngay ý nghĩa của việc Nằm mơ thấy chim bay may mắn – Đánh con gì để thắng lớn một cách bất ngờ? trên website của chúng tôi.
Kết luận
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về khái niệm “3 đường thẳng đồng quy là gì” trong hình học. Nắm vững kiến thức về đồng quy không chỉ giúp bạn giải quyết các bài toán hình học một cách dễ dàng mà còn mở ra những ứng dụng thú vị trong nhiều lĩnh vực của đời sống. Hãy tiếp tục theo dõi website THPT Hồng Ngự 1 để khám phá thêm nhiều kiến thức bổ ích khác. Nếu bạn sinh vào ngày 21 tháng 6 là cung gì, hãy tìm hiểu về cung hoàng đạo của mình trên trang web của chúng tôi nhé!
Có thể bạn quan tâm
- 6789 nghĩa là gì? Giải mã ý nghĩa con số 6789 trong phong thủy
- Hình ảnh Anime dễ thương cặp đôi: Tổng hợp những hình nền đẹp nhất
- Cánh Tay Đòn Của Lực Là Gì? Giải Thích Chi Tiết và Dễ Hiểu
- Tự thụ phấn là gì?
- Những Câu Nói Hài Hước Về Phụ Nữ – Thêm Gia Vị Cho Cuộc Sống
- Trứng Rụng Là Gì? Dấu Hiệu Nhận Biết và Cách Xác Định
- Bắn Cá MM88: Săn Thưởng Lớn, Giải Trí Đỉnh Cao
- 15/4 Âm là bao nhiêu Dương 2022?
- CM trong Bóng Đá Là Gì? Giải Thích Chi Tiết Về Vị Trí Tiền Vệ Trung Tâm
- Huobi Là Gì? Tìm Hiểu Về Sàn Giao Dịch Tiền Điện Tử Huobi
